I made a post about convolution, but I think it's a good, and simple, subject for we start our studies.
Look the noised signal:
-->T = 100;
-->t = 1:T;
-->w = %pi/10;
-->s = cos(w*t); //pure signal
-->n = rand(1, T, 'normal')*0.1; //noise
-->x = s + n;
-->plot(t, x);
The result is:
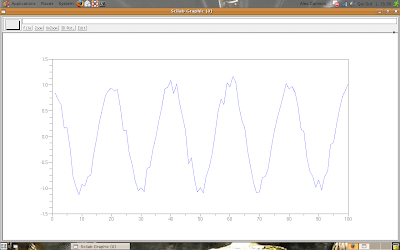
Now, let's filter the signal using an average filter.
We have two options for apply the filtering:
The first
-->Tm = 5;
-->y = [];
-->for i = 1:Tm,
-->y(i) = mean(x(1:i));
-->end;
-->for i = (Tm + 1):T,
-->y(i) = mean(x((i - Tm):i));
-->end;
-->plot(t, y);
The result is:

The second
-->Tm = 5;
-->m = ones(1, Tm);
-->y = convol(x, m);
-->ty = 1:length(y);
-->plot(ty, y);
The result is:
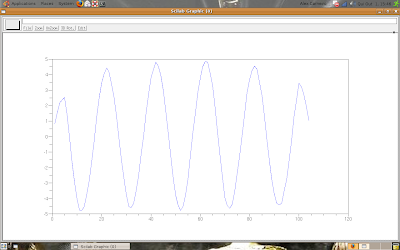
If you make the math operations, you'll see the results are, numerically, the same for t = Tm + 1 until t = T.
4 comments:
wow thank you very much...
your article is very helpful..
i'm student and i want to learn about digital data processing..
can i make real time series (not even or odd) use fourier transform in scilab? please help me. thanks
Fourier Transform is very useful for signal processing, but if you wanna design a real time system I recommend for you using convolution because it's easier to make the model input -> system -> output. However, Fourier Transform should be used for analyzing spectrum of the both signals: input and output.
thank you very much Mr. Sheep.
Mr. Sheep, can you give a tutorial to design a real time system using convolution please?
i'm newbie here. i haven't understood T.T
Unfortunately, I don't have any tutorial for real time signal processing, but you can try in Scilab examples or google about the kind of application you're designing.
Post a Comment