Plotting contours of surfaces

I know there is very useful to see contours of surfaces, many areas use this kind of resource and Scilab has a very simple way to do that.

For a first example, let's use the surface given by the function z = x² + y², this function is a 3D parable. Run the following code for making this surface's graph.


x = -5:0.1:5;
 y = -5:0.1:5;

[xx yy] = meshgrid(x, y);

z = xx.^2 + yy.^2;

plot3d(x, y, z);


The generated graph is like this.

Now, let's see the contours of that surface. But, before, it's interesting to analyze the equation z = x² + y². If z is fixed in a constant value, we have x² + y² = const and this equation means a circle centered in the point (0, 0) and radius square of const.

For plotting the contours, run this code:

n_curves = 10;
x = -5:0.1:5;
y = -5:0.1:5;

function z=my_surface(xx, yy),
z=xx^2 + yy^2;
endfunction

contour(x, y, my_surface, n_curves);


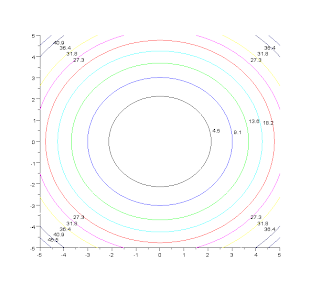
The result is presented following:

In fact, we can see there are concentric circles centered in the point (0, 0).

So, that's all folks!