Last week I was teaching about combinatorial analysis and talking about factorial operator I remembered Gamma Function, this function is very useful in signal processing but particularly Gamma Function is equal to the factorial for non-negative integer numbers.
Theory about Gamma Function is very well described in Wikipedia: http://en.wikipedia.org/wiki/Gamma_function
The equation that defines Gamma Function is
Following figure presents the graph of Gamma Function
And when z is a non-negative integer is verified that
This consequence is because of the property
Typical values of Gamma function are
In Scilab, there are both functions: gamma(.) and factorial(.), following are some examples of these functions
-->factorial(1)
ans =
1.
-->gamma(1)
ans =
1.
-->factorial(1.5)
!--error 10000
factorial: Wrong value for input argument #1: Scalar/vector/matrix/hypermatrix of positive integers expected.
at line 14 of function factorial called by :
factorial(1.5)
-->gamma(1.5)
ans =
0.8862269
-->sqrt(%pi)/2
ans =
0.8862269
Look factorial(.) is not possible to be applied in a non-integer number, the same happens with negative numbers.
And gamma(.) in 1.5 is equal to sqrt(%pi)/2 verifying the correspondence presented in the typical values figure.
Obs.: all equations and figures that I posted in this text were got from the Wikipedia page.
Theory about Gamma Function is very well described in Wikipedia: http://en.wikipedia.org/wiki/Gamma_function
The equation that defines Gamma Function is
Following figure presents the graph of Gamma Function
And when z is a non-negative integer is verified that
This consequence is because of the property
Typical values of Gamma function are
In Scilab, there are both functions: gamma(.) and factorial(.), following are some examples of these functions
-->factorial(1)
ans =
1.
-->gamma(1)
ans =
1.
-->factorial(1.5)
!--error 10000
factorial: Wrong value for input argument #1: Scalar/vector/matrix/hypermatrix of positive integers expected.
at line 14 of function factorial called by :
factorial(1.5)
-->gamma(1.5)
ans =
0.8862269
-->sqrt(%pi)/2
ans =
0.8862269
Look factorial(.) is not possible to be applied in a non-integer number, the same happens with negative numbers.
And gamma(.) in 1.5 is equal to sqrt(%pi)/2 verifying the correspondence presented in the typical values figure.
Obs.: all equations and figures that I posted in this text were got from the Wikipedia page.


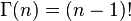


No comments:
Post a Comment